


Physical-mechanical characterization of structural biocomposite sandwich-like panels – A load-bearing wall alternative for non-conventional constructions
Nathaly Andino(1)
Andrés García(1)
Oswaldo Mauricio González(1)(2)
(1) Carrera de Ingeniería Civil, Departamento de Ciencias de la Tierra y Construcción, Universidad de las Fuerzas Armadas – ESPE, Sangolquí, Ecuador. nsandino@espe.edu.ec magarcia19@espe.edu.ec
(2) School of Engineering and Built Environment, Griffith University Gold Coast campus, QLD 4222, Australia m.gonzalezmosquera@griffith.edu.au
Recibido: Junio, 2019
Aceptado: Noviembre, 2019
Doi: http://dx.doi.org/10.24133/ciencia.v22i1.1273
La utilización de materiales tradicionales como elementos de mampostería en construcciones convencionales constituye una de las mayores causas de muerte durante eventos telúricos debido a su efecto de volcamiento. En Ecuador persiste la utilización de estos materiales a pesar de estar localizado en una zona de alto riesgo sísmico, y en un territorio privilegiado en recursos naturales que no son explotados adecuadamente. La presente investigación tiene por finalidad caracterizar físico-mecánicamente prototipos de biotableros estructurales compuestos tipo sándwich como alternativa de pared portante en construcciones no-convencionales que fomenten el desarrollo sustentable de biomateriales de la zona. 46 muestras extraídas de dos prototipos se ensayaron de acuerdo a la normativa vigente ASTM bajo los modos mecánicos de compresión, flexión, tracción y corte con sus respectivas densidades y contenidos de humedad. Los resultados experimentales fueron validados mediante 40 análisis de elementos finitos procesados en el software LSDyna, que a su vez permitieron establecer una proyección de sus capacidades estructurales bajo diferentes condiciones de carga. Los resultados obtenidos reflejan biotableros con una excelente flexibilidad y resistencia mecánica que a su vez se traduce en un alto comportamiento dúctil; lo que permitirá disminuir efectos adversos durante eventos sísmicos de alta magnitud y duración.
Palabras clave:
Caracterización mecánica de biomateriales, madera laminada cruzada, Dendrocalamus asper, modelamiento y análisis de elementos finitos, Ochroma pyramidale.
The use of traditional materials as masonry elements in conventional constructions is one of the major causes of injuries and death due to the overbalance effect produced during telluric events. Nonetheless, traditional materials are still widely used as part of the Ecuadorian construction industry despite the Country is located in both a high-risk seismic region and a territory privileged by natural resources that in turn are not properly exploited. Hence, this research aims to physically and mechanically characterize sandwich-like structural biocomposite panels as feasible alternative for load-bearing walls in non-conventional constructions that promote biomaterials sustainability. To fulfill the purpose in this study and according to the current ASTM standards, 46 samples from two biopanel prototypes were tested under the mechanical modes of compression, bending, tension and shear with their corresponding densities and moisture contents. Furthermore, the experimental results were validated by means of finite element analyses using the LS-Dyna software, to then calculate the biopanel structural capacities under different loading conditions. The acquired results show biopanels with an excellent flexibility and mechanical resistance that in turn reflects high ductile performance during progression of stresses; this will definitely allow reducing the abovementioned adverse effects during seismic events of high magnitude and duration.
Key words:
Biomaterial mechanical characterization, cross laminated timber, Dendrocalamus asper, engineered wood products, finite element modeling and analysis, Ochroma pyramidale.
El Ecuador, ubicado en una de las zonas de mayor riesgo sísmico del mundo, presenta una recurrencia de eventos telúricos cuyas magnitudes superan los 7 grados en la escala de Richter, los mismos que son provocados por procesos de subducción de la placa de Nazca bajo la placa Sudamericana (Hibsch et al., 1996) . Según Rivadeneira et al. (2007), en el territorio ecuatoriano se han registrado más de 37 terremotos durante los últimos 458 años, con efectos destructivos y catastróficos [6,2 - 6,95 y > 8 grados en la escala de Richter, respectivamente (Stein & Wysession, 2009)]; a esta estadística se añaden 96 eventos sísmicos si se toman en cuenta los sismos con magnitudes inferiores a 7 grados en la escala de Richter.
El 16 de abril del 2016 se registró el evento sísmico de carácter catastrófico más reciente (7,8 grados en la escala de Richter), cuyo epicentro se localizó en la ciudad de Pedernales, provincia de Manabí. El evento sísmico ocasionó graves daños en zonas con altos niveles de pobreza, dejando un saldo de 35000 viviendas afectadas, de las cuales 19500 quedaron totalmente destruidas; resultado de ello 670 muertos y 6300 heridos (Secretaria de Gestion de Riesgos, 2016). En las zonas afectadas por el sismo predominaban edificaciones construidas con materiales convencionales (hormigón armado con paredes de bloque o ladrillo y estructuras de acero) que si bien presentan beneficios en cuanto a resistencia y durabilidad, al no contar con diseños adecuados y al presentar falencias durante el proceso constructivo, solo agravaron los efectos destructivos del sismo.
En el evento sísmico de abril del 2016, referido en este estudio como el “terremoto de las mamposterías”, el efecto de volcamiento ocasionado por la falla de las mamposterías de bloque y/o ladrillo causaron la mayor cantidad de muertos y heridos debido a su capacidad limitada en términos dinámicos y mecánico-estructurales; es decir, no están diseñadas para resistir y disipar cargas sísmicas (Páez, 2016). Adicional al problema mencionado, se suma que los materiales convencionales ocasionan un alto grado de contaminación ambiental durante sus fases de extracción y procesamiento de materias primas; es así que la industria de la construcción es la segunda en el país (después de la industria manufacturera) en emitir gases contaminantes al producir alrededor de 319.402 toneladas de gases al año entre ellos dióxido de Carbono (CO2), cifra que aumenta periódicamente debido a prácticas ineficientes y tradicionales que no priorizan la conservación del medio ambiente (Ministerio del Ambiente, 2014). En este contexto, la construcción con biomateriales representa en la actualidad una alternativa eficiente; de hecho, construcciones de acero y concreto son 26% y 31%, respectivamente, más contaminantes que construcciones en base a cualquier tipo de biomaterial (Lippke et al., 2010). En efecto, países como Estados Unidos de América, Australia, Canadá, Japón, Inglaterra y Chile, cuentan con estándares constructivos que permiten realizar edificaciones de gran envergadura en base a biomateriales, siendo elementos derivados de diferentes especies de madera o residuos de ella, los que son más utilizados bajo el nombre de engineered wood products [EWP, (McKeever, 1997)]. En el Ecuador sin embargo, y a pesar de ser un país privilegiado en recursos naturales como la madera antes referida, no se han implementado soluciones técnicas que permitan modernizar los sistemas constructivos tradicionales en base a biomateriales, debido al desconocimiento de sus capacidades y potenciales aplicaciones; desaprovechando así más de 7 millones de hectáreas de especies forestales disponibles, entre las cuales se puede citar al bambú, palma de coco y balsa (Salazar 2014). Es de gran relevancia entonces, proponer sistemas que incluyan soluciones estructurales con elementos innovadores que cumplan con requerimientos de ingeniería y medio ambiente. La presente investigación tiene por objeto caracterizar las propiedades físicomecánicas, así como analizar el comportamiento biomecánico y estructural de biotableros estructurales tipo sándwich compuestos de un núcleo de Ochroma pyramidale (balsa) y paneles externos bidireccionales de Dendrocalamus asper (bambú), para proponer su aplicación como pared estructural en construcciones ubicadas en zonas de alto riesgo sísmico.
Se diseñaron 2 prototipos de biotableros: (i) prototipo 1 [PB1, (1200 mm x 600 mm x 74 mm)] y prototipo 2 [PB2,
(1200 mm x 600 mm x 124 mm)]. La figura 1 presenta la configuración del tablero estructural compuesto tipo
sándwich, la misma que consta de un núcleo de balsa y 3 láminas bidireccionales de bambú que conforman los
paneles externos.
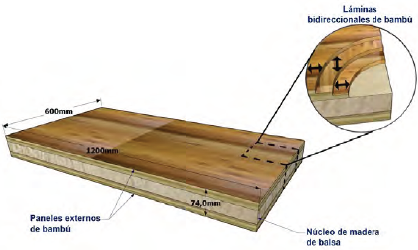
Figura 1. Prototipo de tablero estructural compuesto tipo sándwich elaborado con balsa y bambú.
Las láminas de bambú [módulo de elasticidad (MOE) paralelo a la fibra de 7420 MPa, densidad básica (db) de
658,42 kg/m3 al 14% de contenido de humedad (C.H)] se obtuvieron de un espécimen de aproximadamente 4 años
de edad y 20 cm en promedio de diámetro exterior, que fue sometido a un proceso de latillado, curado, secado
y cepillado. Se utilizó resina vinil acrílica como agente de unión entre latillas, mismas que se sometieron a una
presión de 300 psi a 100°C durante 30 minutos para conformar el panel externo. El panel de núcleo de balsa tipo
BALTEK® [módulo de elasticidad (MOE) paralelo a la fibra de 2526 MPa, densidad básica (db) de 148 kg/m3 al
12,6% de contenido de humedad (C.H)] se unió a los paneles externos con poliuretano de 2 componentes (Pur2C)
para posteriormente prensarlo bajo los mismos parámetros de presión, temperatura y tiempo antes descritos, y así
conformar el tablero compuesto como tal.
Los ensayos de laboratorio para caracterizar mecánicamente a los prototipos propuestos, se llevaron a cabo en
una máquina de ensayos universales (UTM) de 300 kN de capacidad, marca AGS-X Shimadzu, equipada con un video-extensómetro digital de procedencia japonesa [2 cámaras de alta resolución marca Kowa (f=25mm/F1,4 y
HR F2,8/5mm)] para medir deformaciones unitarias; estos datos de deformación fueron verificados a través del
uso de extensómetros de lámina (strain gauges) de 5 mm, adheridos a cada muestra mediante resina poliepóxido
activada con un agente catalizador. Finalmente, para decodificar la información del extensómetro se utilizó un
puente medidor de deformaciones Wheatstone marca Omega de 120 ohmios.
3.1. 3.1. MODO MECÁNICO DE COMPRESIÓN
En concordancia con la ASTM C364/C364M-16 Standard Test Method for Edgewise Compressive Strength of Sandwich Constructions, un total de 10 muestras sin defectos se ensayaron bajo el modo mecánico de compresión, 5 correspondientes al prototipo 1 (150 mm x 150 mm x 74 mm) y 5 del prototipo 2 (250 mm x 250 mm x 124 mm), como se muestra en la figura 2.

Figura 2. Muestras de tablero estructural compuesto tipo sándwich para pruebas de compresión (a) direcciones de carga, (b) muestra nominal del prototipo 1 y (c) muestra nominal del prototipo 2.
El ensayo consistió en la aplicación de carga axial sobre la muestra de tablero compuesto tipo sándwich, para esto la platina inferior de la UTM Shimadzu estuvo completamente fija, mientras que la placa superior (17 mm de espesor) se acopló sobre una rótula esférica para distribuir uniformemente la carga sobre la muestra. Para evitar los efectos de fricción entre la muestra y la máquina se colocó polvo de grafito entre las placas de carga y la muestra. El cabezal de la máquina se desplazó a una velocidad constante de 0.5 mm/min, logrando un tiempo de ensayo promedio comprendido entre 3 y 6 minutos. Debido a la reducción de la fricción entre placas y muestra, se anulan las tensiones producidas en el plano perpendicular, por lo tanto aplica la ley de Hooke (Ugural, 2008) a fin de calcular el módulo de elasticidad (MOE) en función del esfuerzo normal (σ) y la deformación unitaria (ε), como se indica en la ecuación 1.
![]()
Aplicando el principio antes descrito, se determinó el módulo de elasticidad (MOE) en MPa, como la pendiente del rango lineal elástico de la curva esfuerzo-deformación unitaria; este valor es calculado únicamente bajo el presente modo mecánico ya que es una característica del material y no depende del tipo de aplicación de carga.
El módulo de ruptura en la dirección longitudinal [MORL, ver figura 2a], es la capacidad máxima que tiene un material para soportar cargas de tipo axial (Ugural, 2008), y en el presente estudio se lo calcula en base a la norma ASTM C364, mediante la ecuación 2.
![]()
donde MOR L está dado en MPa, Fc_max es la fuerza máxima en N, obtenida en el ensayo de compresión antes de que la muestra presente fallo mecánico, w es el ancho de la muestra en mm y f es el espesor de cada panel externo en mm.
3.2. MODO MECÁNICO DE FLEXIÓN
De acuerdo a la ASTM C393 Standard Test Method for Core Shear Properties of Sandwich Constructions by Beam Flexure, un total de 10 muestras libres de defectos se ensayaron bajo el modo mecánico de flexión, de las cuales 5 muestras se tomaron del prototipo 1 (150 mm x 300 mm x 74 mm) y 5 muestras del prototipo 2 (250 mm x 500 mm x 124 mm) mm, como se muestra en la figura 3.

Figura 3. Muestras de tablero estructural compuesto tipo sándwich para pruebas de flexión (a) direcciones de carga, (b) muestra nominal del prototipo 1 y (c) muestra nominal del prototipo 2.
La configuración del ensayo de flexión a cuatro puntos, se realizó sobre dos apoyos fijos, en los cuales se colocó la muestra centrada para posteriormente aplicar carga mediante dos barras perpendiculares ubicadas equidistantemente sobre el tercio medio de la longitud entre apoyos (S); en los puntos de contacto entre muestra y barras de carga se colocaron almohadillas de caucho de 25 mm de ancho, 3 mm de espesor y 60 de dureza para evitar el daño local. La aplicación de carga se realizó a una velocidad constante de 0.5 mm/min durante un tiempo de ensayo comprendido entre 3 y 6 minutos.
El módulo de ruptura a flexión (MORflex) se define como la capacidad máxima de carga a flexión del tablero sándwich antes de llegar al fallo mecánico, éste parámetro se determinó en base a la ecuación 3 obtenida de la norma ASTM C393 como,
![]()
donde, Fflex_max es la máxima fuerza en N, ejercida sobre la muestra previo al fallo mecánico del material, S es la longitud entre las barras de apoyo fijo en mm, f es el espesor de cada panel externo en mm, c es el espesor del panel de núcleo de balsa en mm, w es el ancho de la muestra en mm y d es el espesor total de la muestra en mm.
En los tableros compuestos tipo sándwich sometidos ante esfuerzos de flexión la falla predominante se da por corte en el material del núcleo, es por tanto preponderante el cálculo del esfuerzo máximo de corte (τmax), mismo que se especifica en la norma ASTM C393, como se indica en la ecuación 4 (cuyos parámetros fueron previamente definidos en el párrafo anterior).
![]()
3.3. MODO MECÁNICO DE TRACCIÓN
Conforme a la ASTM C297 Standard Test Method for Flatwise Tensile Strength of Sandwich Constructions, un total de 10 muestras libres de defectos se ensayaron bajo el modo mecánico de tracción, 5 muestras del prototipo 1 (50 mm x 50 mm x 74 mm) y 5 muestras del prototipo 2 (50 mm x 50 mm x 124 mm), como se muestra en la figura 4.
Previo al inicio del ensayo y para garantizar la distribución uniforme de la fuerza de tracción entre las muestras y la UTM, se adhirieron bloques de carga metálicos a los paneles externos usando masilla plástica poliéster. Posteriormente se colocó la muestra entre mordazas a presión y se aplicó carga de tracción progresiva perpendicular al plano de los paneles externos. La aplicación de carga se realizó a una velocidad constante de 1 mm/min durante un tiempo comprendido entre 3 y 6 minutos.

Figura 4. Muestras de tablero estructural compuesto tipo sándwich para pruebas de tracción (a) muestra nominal del prototipo 1 y (b) muestra nominal del prototipo 2.
El módulo de ruptura del modo mecánico de tracción (MORtr) refleja la máxima capacidad de resistir esfuerzos de tracción aplicados en sentido perpendicular al plano de los paneles externos (Ugural, 2008); este valor se calculó según la norma ASTM C297, mediante la ecuación 5,
![]()
donde, FT_max es la máxima fuerza de tracción en N, aplicada sobre la muestra previo al fallo mecánico del núcleo y A es la sección transversal en mm2 sobre la que actúa la carga.
3.4. MODO MECÁNICO DE CORTE
Según la normativa ASTM C273, Standard Test Method For Shear Properties of Sandwich Core Materials, un total de 10 muestras libres de defectos se ensayaron ante la acción de esfuerzos de corte, 5 del prototipo 1 (60 mm x 310 mm x 74 mm) y 5 del prototipo 2 (60 mm x 310 mm x 124 mm) , como se muestra en la figura 5.
Previo al ensayo de corte se adhirieron placas metálicas a las muestras mediante el uso de masilla plástica poliéster para asegurar que los esfuerzos de corte generados se transfieran al material de núcleo. Posteriormente, se colocó la muestra en la UTM dándole el ángulo necesario para que el plano de acción de la fuerza pase por los extremos de la muestra (entre 21° y 33,5° de desviación respecto al eje axial de aplicación de fuerza). La aplicación de carga se realizó a una velocidad constante de 0.5 mm/min, durante un tiempo de ensayo comprendido entre 3 y 6 minutos.

Figura 5. Muestras de tablero estructural compuesto tipo sándwich para pruebas de corte (a) muestra nominal del prototipo 1 y (b) muestra nominal del prototipo 2.
El esfuerzo máximo de corte (τmax) se calculó de acuerdo a la norma ASTM C273 en base a la ecuación 6,
![]()
donde Fs_max es la fuerza máxima de corte en N ejercida sobre la muestra previo al fallo mecánico del núcleo, L es la longitud de la muestra en mm y w es el ancho de la muestra en mm.
El módulo de corte (G) es la propiedad que refleja la resistencia del material de núcleo ante deformaciones de corte producidas por la aplicación de cargas, mismo que se calcula de acuerdo a la normativa ASTM C273 mediante la ecuación 7.
![]()
donde, M es la pendiente del rango lineal elástico de la curva esfuerzo de corte-deformación unitaria, c es el espesor del núcleo de balsa en mm, L es la longitud de la muestra en mm y w es el ancho de la muestra en mm.
3.4 MODELAMIENTO Y ANÁLISIS DE ELEMENTOS FINITOS
Los materiales de mampostería tradicional (bloques y ladrillos) son sumamente afectados por la acción de movimientos telúricos, es decir no se comportan adecuadamente ante la aplicación de cargas cíclicas (ver figura 6), generando dos tipos de mecanismos de fallo que son (i) fuera y (ii) dentro del plano (Carrillo & González, 2007, Varela-Rivera et al., 2015).
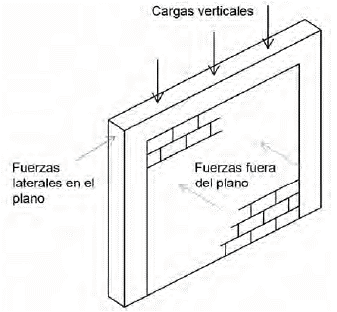
Figura 6. Tipo de cargas actuantes en pórticos con mampostería no reforzada.
Los fallos fuera del plano, comúnmente se producen por la falta de anclaje de muros a diafragmas de techo y piso, esta falla tiende a ser súbita disminuyendo la capacidad de resistir cargas gravitatorias. Por otro lado, los fallos dentro del plano, se producen por esfuerzos excesivos de cortante y flexión (ver figura 7), agravando su capacidad de resistencia y ocasionando en la mayoría de los casos el colapso de las estructuras de mampostería no reforzada (Carrillo & González, 2007, Varela-Rivera et al., 2015).
En contraste, los biotableros estructurales tipo sándwich propuestos en esta investigación trabajan tanto dentro como fuera del plano, siendo este último comportamiento el más peligroso para esta clase de materiales (tipo relleno). Con el fin de determinar el comportamiento ante fallas dentro y fuera del plano, así como la validación y ajuste de resultados experimentales a través de factores de compensación (FC), se procedió a elaborar modelos de elementos finitos en base a los modos mecánicos preponderantes de compresión y flexión.
Previo al desarrollo de los modelos de elementos finitos (FEM), se asumieron suposiciones en base a la teoría de tableros compuestos tipo sándwich expuesta por Davies (1987) donde (i) se considera que los materiales componentes del tablero sándwich (paneles externos y panel de núcleo) trabajan únicamente en el rango lineal elástico, (ii) el panel de núcleo permite que el esfuerzo de corte sea constante a través de su estructura, (iii) no existe delaminación entre los materiales componentes del tablero tipo sándwich y (iv) el panel de núcleo no presenta deformación en dirección transversal.
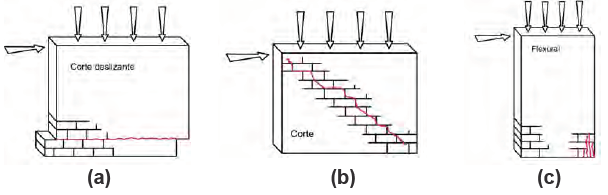
Figura 7. Modos de fallo típico de mampostería no reforzada sometida a cargas en el plano (a) Corte deslizante, (b) Corte Puro y (c) Falla Flexural con destrucción en la esquina. Modificado de (Garbin et al., 2007)
El modelamiento computacional de cada modo mecánico se realizó en el software LS-Dyna®. En los modelos de elementos finitos (FEM) se asignaron las dimensiones geométricas y las direcciones de fibra de cada muestra ensayada. Las condiciones de borde en cada FEM se asignaron en función de los ensayos de laboratorio, es decir en la prueba de compresión se empotraron todos los nodos inferiores del modelo, mientras que en flexión se simularon dos apoyos móviles con nodos restringidos, de modo que ambos sistemas de modelamiento estructural tuvieron 1 grado de libertad (ver figura 8).
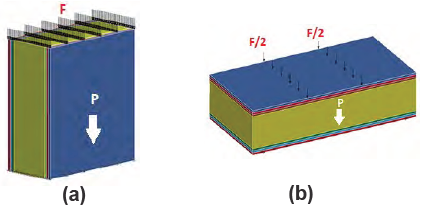
Figura 8. Condiciones geométricas, condiciones de borde y condiciones de carga en los modelos de elementos finitos (a) modo mecánico de compresión y modo mecánico de flexión.
Las propiedades físicas (densidad y contenido de humedad) y mecánicas (MOE, MORL, MORflex, τmax y G) utilizadas en la elaboración de cada FEM se derivaron de los ensayos de laboratorio. Las propiedades de los materiales que no se determinaron a través de caracterización mecánica se obtuvieron de Ross (2010).
La modelación computacional comprendió un total de 40 análisis estático-no lineales que consideraron los efectos geométricos no-lineales resultado de las altas deflexiones y desplazamientos de cada FEM. El comportamiento ortotrópico y anisotrópico de los materiales componentes del tablero estructural tipo sándwich, así como la dirección de sus fibras se lograron replicar mediante un mallado de elementos hexaédricos tridimensionales de 8 nodos, mismos que permitieron calcular los esfuerzos generados en el centroide del elemento, basándose en la integración de Gauss de 8 puntos.
En el análisis finito de elementos (FEA) se consideraron dos condiciones de carga (i) fuerza de compresión axial paralela al plano de los paneles externos (compresión) y (ii) fuerza de flexión perpendicular al plano de paneles externos (flexión), en ambos casos denominada como (F).
Durante la fase de caracterización mecánica se estableció que los prototipos estudiados tienen un comportamiento elástico hasta que llegan al punto de fluencia, por lo tanto, la teoría de análisis de progresión de esfuerzos utilizada en esta investigación fue la de Von Mises (Hull & Clyne, 1996), en donde la falla del material se asume cuando la progresión de esfuerzos (energía de distorsión) rebasa la capacidad de resistecia mecánica del material (MOR), y se representa mediante un índice de falla (FI), por lo que, cuando FI ≥1, se evidencia el inicio de falla del material en términos de mecánica estructural.
Una vez determinado el FEM óptimo (mediante el estudio de convergencia respectivo para cada modo mecánico), se procede al análisis finito de elementos respectivo con la finalidad de obtener los factores de compensación (ver ecuación 8) para los valores de resistencia a cargas máximas de compresión y flexión.
![]()
donde, es el módulo de ruptura en MPa obtenido de cada FEA y es el módulo de ruptura experimental en MPa.
3.6. ANÁLISIS ESTRUCTURAL DE TABLEROS TIPO SÁNDWICH
Con la finalidad de establecer la aplicación estructural que tienen los prototipos propuestos en base a su comportamiento mecánico, es necesario determinar la carga axial admisible, carga lateral admisible y rigidez lateral de los mismos.
3.6.1. CARGA AXIAL ADMISIBLE.
La máxima carga axial (antes del fallo mecánico por pandeo) que soportan los tableros estructurales tipo sándwich se determinó mediante el cálculo de la carga crítica de Euler misma que para tableros tipo sándwich se fundamenta en la ecuación 9 dada por Allen (2013),
![]()
donde, Pcr es la carga crítica por pandeo en kg, Lef2 es la longitud efectiva de una columna equivalente con articulaciones en sus extremos en mm2 y D es la rigidez a flexión de los elementos del tablero tipo sándwich, misma que según Allen (2013), se calcula mediante la ecuación 10.
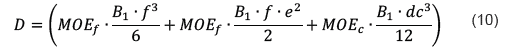
donde, es el módulo de elasticidad de los paneles externos en kg/cm2, es el módulo de elasticidad del panel de núcleo en kg/cm2, es el ancho medido de la muestra en cm, es el espesor del panel externo en cm, es la profundidad del material del núcleo en cm, y es la distancia entre los centroides de los paneles externos en cm.
En la fase de caracterización mecánica las muestras ensayadas bajo el modo mecánico de compresión presentaron falla por aplastamiento de los paneles externos debido a que la longitud efectiva de las muestras fue muy corta para llegar a producir pandeo de las mismas; por consiguiente, se hace necesario determinar la carga admisible incluyendo el efecto de pandeo en los prototipos en base a las dimensiones reales con las cuales serán empleados en obra. Con el fin de proyectar la carga crítica de pandeo (Pcr1) de las muestras ensayadas en laboratorio, hacia la correspondiente (Pcr2) de los tableros de dimensiones estándar (1200 mm x 600 mm x d), se realizó una derivación de las ecuaciones 9 y 10, misma se representa por la ecuación 11.
![]()
3.6.2. CARGA LATERAL ADMISIBLE
La rigidez lateral de un tablero estructural compuesto tipo sándwich se define como la capacidad del mismo para resistir la aplicación de cargas laterales sin presentar deformación (Terradillos López, 2018). Este parámetro se calculó en base a la modelación del tablero propuesto en el programa SAP 2000®, determinando la carga necesaria para producir 1 cm de deformación horizontal (rigidez lateral). Al obtener la rigidez lateral del prototipo se realiza la derivación matemática de la Ley de Hooke (ver ecuación 1) y el esfuerzo mecánico de un material (ver ecuación 12) para obtener la carga lateral admisible (ver ecuación 13),
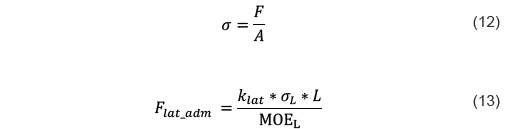
donde, σL es el esfuerzo lateral aplicado en MPa, MOEL es el módulo de elasticidad en dirección longitudinal en MPa, ε es la deformación unitaria, Flat_adm es la carga lateral admisible en N, A es el área perpendicular a la aplicación de la carga en mm2, klat es la rigidez lateral del tablero en N/mm, y L es la longitud en la dirección axial del tablero de dimensión estándar en mm. Los resultados del análisis estructural de los tableros compuestos tipo sándwich propuestos fueron la base para determinar las potenciales aplicaciones de los mismos en proyectos de construcción no-convencional en zonas de alto riesgo sísmico.
4.1. MODO MECÁNICO DE COMPRESIÓN
Los resultados promedio de las muestras ensayadas a compresión en dirección paralela al plano longitudinal – radial (L-R) se presentan en la tabla 1 y la figura 9.
Tabla 1. Resultados promedio de ensayos de compresión en muestras extraídas de los prototipos de tableros estructurales tipo sándwich

Según los valores presentados en la tabla 1, se desprende que el prototipo PB2 tiene las mejores características de flexibilidad; mientras que en términos de resistencia a esfuerzos, ambos prototipos se encuentran dentro del mismo rango de valores. Además los resultados evidencian coeficientes de variación mínimos (≤ 0,06) lo cual refleja un porcentaje mínimo de error en los valores obtenidos en laboratorio, y por consiguiente, una baja dispersión de resultados en relación al valor promedio de todas las muestras ensayadas.
La figura 9 grafica el esfuerzo de compresión (σL) versus la deformación unitaria (ε) en el plano (L-R) de las muestras ensayadas. Se puede observar que el comportamiento mecánico tanto en el rango lineal elástico como en el plástico es similar para todas las muestras ensayadas; además, los resultados evidencian un alto comportamiento dúctil [capacidad del material y sus componentes para soportar una deformación plástica antes de llegar al fallo mecánico] ante la aplicación de carga axial progresiva.
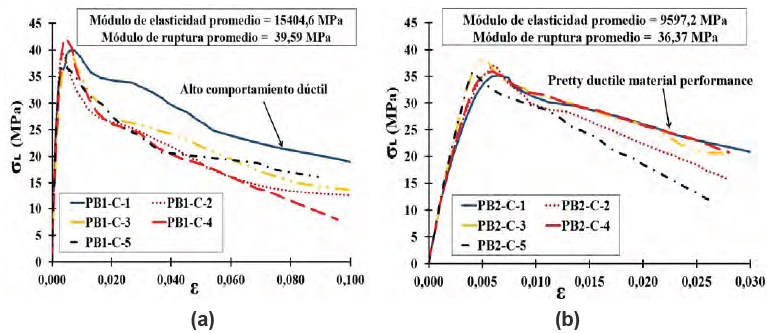
Figura 9. Esfuerzo de compresión – deformación unitaria en dirección paralela a la aplicación de carga (a) prototipo 1 y (b) prototipo 2.
Las muestras ensayadas bajo el modo mecánico de compresión evidenciaron una falla por aplastamiento de los paneles externos, ya que al presentar mayor rigidez, estos absorben las mayores solicitaciones de carga en este modo mecánico (ver figura 13).
4.2. MODO MECÁNICO DE FLEXIÓN
Los resultados de las muestras ensayadas a flexión en el plano radial transversal (R-T) se presentan en la tabla 2 y la figura 10.
Tabla 2. Resultados promedio de ensayos de flexión en muestras extraídas de los prototipos de tableros estructurales tipo sándwich

Los resultados denotan que los dos prototipos presentan valores muy similares de resistencia ante la progresión de cargas de flexión; esto se debe a que la diferencia entre espesores de los paneles externos de los dos prototipos es de tan solo 2 mm. En términos de resistencia a esfuerzos de corte, la diferencia se produjo debido a que el tablero PB2 poseía un núcleo de balsa 50 mm mayor que el prototipo PB1 lo cual impidió la correcta transferencia de corte entre elementos. Los coeficientes de variación obtenidos en base a los resultados de la tabla 2 presentaron un valor máximo de 0.20, el cual denota una leve dispersión de resultados producto de la gran deformación que sufren las muestras en el modo mecánico de flexión, lo cual no sucede en el modo mecánico de compresión debido a que las deformaciones son muchísimo menores.
La figura 10 grafica la fuerza de flexión versus el desplazamiento experimentado en cada muestra; el comportamiento mecánico (tanto en el rango lineal elástico como en el plástico) de las muestras extraídas de los prototipos PB1 y PB2 fue uniforme ante la aplicación de cargas de flexión, presentando alta ductilidad después de llegar al máximo valor de resistencia, de modo que no existió falla total del prototipo durante el ensayo.
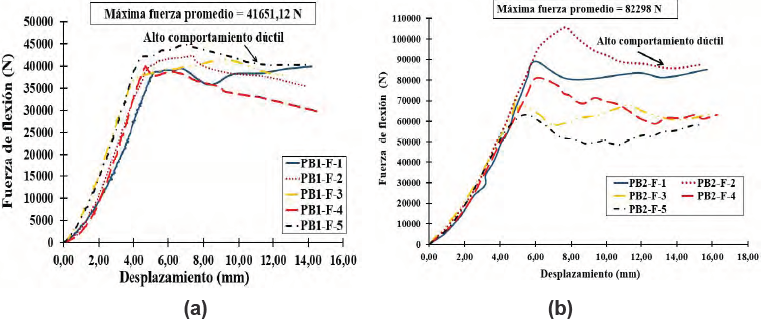
Figura 10. Fuerza de flexión – desplazamiento en dirección perpendicular al plano de los paneles externos (a) prototipo 1 y (b) prototipo 2.
La falla predominante en el modo mecánico de flexión fue por cizalla en el núcleo, para después evolucionar hacia una falla por ligante entre paneles externos y panel de núcleo (ver figura 14).
4.3. MODO MECÁNICO DE TRACCIÓN
Los resultados promedio de módulo de ruptura a tracción (MORtracción) calculados para las muestras ensayadas de los prototipos PB1 y PB2, en dirección perpendicular al plano longitudinal – radial (L-R) se presentan en la tabla 3 y la figura 11.
Tabla 3. Resultados promedio de ensayos de tracción en muestras extraídas de los prototipos de tableros estructurales tipo sándwich

La figura 11 indica que la tendencia de comportamiento mecánico de las muestras ensayadas a tracción es uniforme, asimismo se puede apreciar que existe una falla frágil total al momento que las muestras alcanzan su máxima capacidad de resistencia a cargas de tracción. Las totalidad de las muestras ensayadas evidenciaron una falla recurrente por tracción de los paneles externos, la cual se debe a que el ligante utilizado en su elaboración (resina vinil acrílica) no proporcionó una resistencia óptima ante este tipo de progresión de esfuerzos.
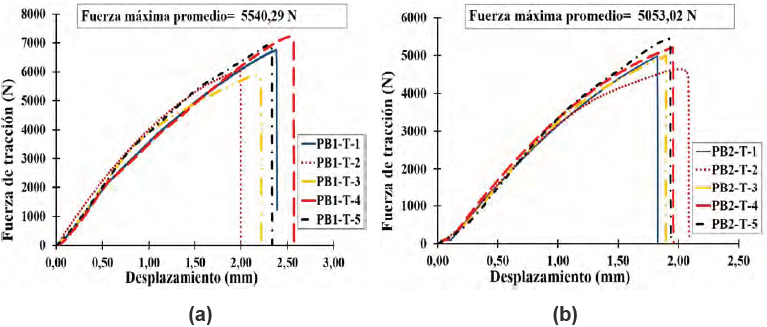
Figura 11. Fuerza de tracción – desplazamiento en dirección perpendicular al plano de los paneles externos (a) prototipo 1 y (b) prototipo 2.
4.4. MODO MECÁNICO DE CORTE
Los resultados promedio de esfuerzo de corte (τmax) y módulo de corte (G) calculados para las muestras ensayadas de los prototipos PB1 y PB2, se presentan en la tabla 4 y figura 12.
Tabla 4. Resultados promedio de ensayos de corte en muestras extraídas de los prototipos de tableros estructurales tipo sándwich

Los resultados indican que el prototipo PB1 presenta las mejores características en este modo mecánico, con un módulo de corte que refleja mayor rigidez y un valor de resistencia a esfuerzo máximo de corte muy semejante al de PB2.
La figura 12 presenta una tendencia de comportamiento mecánico similar en todas las muestras ensayadas; asimismo, se puede apreciar que existe un rango elástico inicial acompañado de una deformación plástica “tipo plateau” que posteriormente desemboca en una falla total del elemento, lo cual implica que ante un esfuerzo de corte (esto es, por cargas de viento y sismo) los tableros estructurales tipo sándwich se comportarían de forma óptima, permitiendo así el desalojo de las estructuras previo a un colapso total.
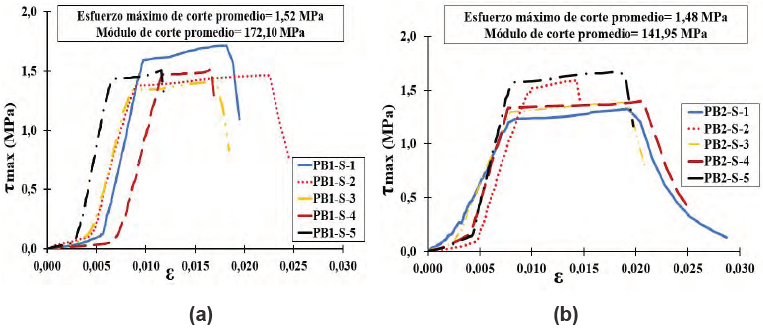
Figura 12. Esfuerzo máximo de corte - deformación unitaria (a) prototipo 1 y (b) prototipo 2
Todas las muestras ensayadas bajo este modo mecánico presentaron falla por corte del núcleo de balsa, misma que se produce debido a la diferencia de rigideces entre los materiales que componen el prototipo de tablero estructural tipo sándwich.
4.5. MODELAMIENTO DE ELEMENTOS FINITOS
En base a los resultados máximos promedio de la caracterización mecánica se identifica como modo mecánico preponderante al de compresión, debido a que es 2,74, 17,92 y 24,57 veces superior a los modos mecánicos de flexión, tracción y corte, respectivamente. Por consiguiente, los resultados de esta sección se enmarcan a los modos mecánicos de compresión y flexión.
De la validación de resultados en base al FEA de cada muestra ensayada bajo el modo mecánico de compresión, se llegó a determinar factores de compensación de 1,08 y 1,04 para PB1 y PB2, respectivamente. De manera similar en el modo mecánico de flexión, se determinaron FC de 1,02 y 1,12 para PB1 y PB2, respectivamente. Los valores de MORL y MORflex compensados se pueden observar en las tablas 1 y 2, respectivamente. Se debe resaltar también que se determinó un valor máximo de 12% de dispersión entre los resultados de FEA y los correspondientes a laboratorio, lo cual denota que los datos experimentales fueron obtenidos de manera muy precisa.
Los FEA permitieron también observar de manera gráfica y en 3D la progresión de esfuerzos y dispersión de los mismos dentro de cada FEM (ver figura 13 y figura 14) lo cual permitió entender de manera lógica el comportamiento mecánico de los elementos propuestos ante las solicitaciones en estudio.
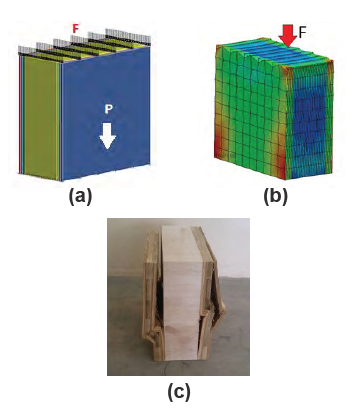
Figura 13. Análisis de elementos finitos modo mecánico de compresión (a) FEM previo a la aplicación de carga (b) progresión de esfuerzos en el FEM y (c) falla por aplastamiento de paneles externos.
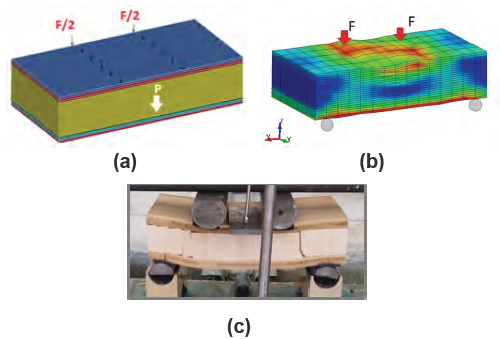
Figura 14. Análisis de elementos finitos modo mecánico de flexión (a) FEM previo a la aplicación de carga (b) progresión de esfuerzos en el FEM y (c) falla por cizalla en el panel de núcleo.
4.6. ANÁLISIS ESTRUCTURAL
La tabla 5 presenta una proyección de 14 propuestas de tableros estructurales compuestos tipo sándwich de diferentes espesores, derivada de los resultados de carga axial admisible, rigidez lateral y carga lateral admisible de los prototipos PB1 y PB2. En estas propuestas, se varía únicamente el espesor del panel de núcleo de balsa, para así incrementar progresivamente su flexibilidad sin un aumento excesivo de peso.
Los resultados presentados en la tabla 5 proyectan la elección y utilización de tableros estructurales compuestos tipo sándwich dependiendo de los esfuerzos admisibles a los cuales se verán abocados al momento de su implementación en la construcción.
Tabla 5. Proyección de características estructurales en tableros compuestos tipo sándwich elaborados de bambú y balsa
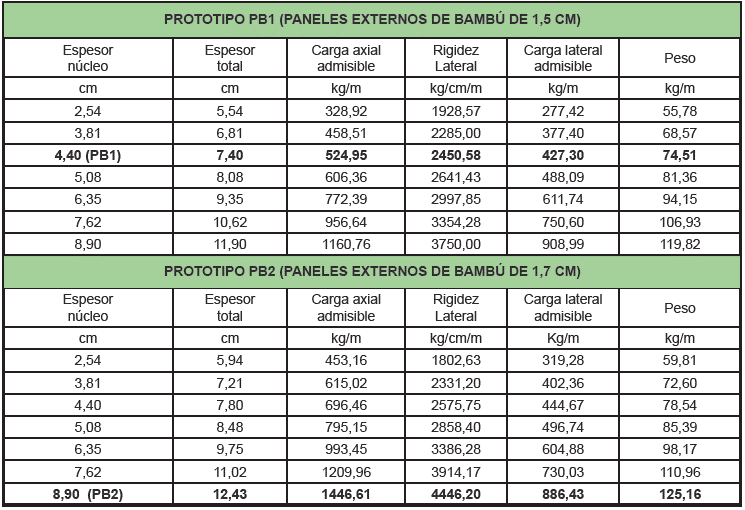
*Los valores resaltados corresponden a los prototipos PB1 y PB2 estudiados en esta investigación.
Los prototipos estudiados se enmarcan en un rango de densidad promedio que va de 291,01 a 413,97 kg/m3, por lo que según Heiko & Barbu (2010) se los clasifica dentro del rango de materiales compuestos ligeros (d ≤ 500 kg/m3). De los resultados obtenidos y en base a los estudios relacionados de González (2016), González (2018), se puede inferir que existe una relación directa entre la densidad y las propiedades mecánicas de los biotableros investigados en este estudio. Los resultados denotan que el ligante utilizado para unir los paneles externos con el panel de núcleo presentó un excelente comportamiento de modo que la delaminación producida entre elementos fue limitada y controlada.
Según los resultados presentados en la tabla 1 se observa una considerable diferencia entre el prototipo PB1 y PB2 en términos de rigidez, siendo el prototipo PB1 1.60 veces más rígido que el prototipo PB2; lo cual refleja una capacidad a flexión superior de PB2 debido a que el espesor del núcleo de balsa (46 mm > PB1) le otorga mayor performance de deformación ante la acción de solicitaciones de carga externa e interna. Asimismo, en términos de resistencia mecánica, los resultados de PB1 y PB2 se enmarcan en valores similares en todos los modos mecánicos analizados; esto debido a que los espesores de los paneles externos de bambú difieren únicamente en 2 mm uno respecto de otro. Por consiguiente, los biotableros propuestos alcanzan un equilibrio adecuado entre flexibilidad y resistencia mecánica, siendo los paneles externos bidireccionales de bambú los que brindan alta resistencia a esfuerzos mientras que el panel de núcleo de balsa le otorga flexibilidad e incrementa su inercia [capacidad de los cuerpos para resistir un cambio en el estado físico de los mismos (deformaciones y giros)] reduciendo el efecto de volcamiento producido por elementos de mampostería tradicional, y por consiguiente, disminuyendo el riesgo de fatalidades durante terremotos.
De la caracterización mecánica de los prototipos PB1 y PB2, se desprende que los biotableros propuestos trabajan en todos los modos mecánicos, lo cual es un plus en comparación con elementos convencionales para pared, ya que en su mayoría son diseñados para compresión. A esto hay que añadir que, la resistencia de los biotableros propuestos bajo los modos mecánicos de compresión y flexión presentan una gran ductilidad en el rango plástico del material compuesto, lo cual es esencial en materiales y elementos a ser utilizados en zonas propensas a eventos telúricos de alta magnitud y duración. Específicamente, de todas las opciones presentadas en la tabla 5, el prototipo PB2, con un espesor total de 12,43 cm [panel de núcleo de balsa = 8,90 cm y espesor de paneles externos= 1,7 cm c/u] presenta los valores más altos respecto de todos los parámetros analizados; por lo tanto, se recomienda su uso como pared portante externa en construcciones expuestas a velocidades críticas de viento (v>17,4 m/s) en zonas de alto riesgo sísmico. No obstante, todas las opciones presentadas en la tabla 5 son aptas para su uso en la construcción.
Es necesario resaltar que el módulo de ruptura promedio a compresión para el prototipo PB2 (MORL= 36.37 MPa) es 2.63 y 1.45 veces superior al de materiales tradicionales como los bloques huecos de hormigón clase A (σadm= 13.8 MPa) y ladrillo macizo tipo A (σadm = 25 MPa), respectivamente. Mientras que el módulo de ruptura a flexión del prototipo PB2 (MORflex= 13.27 MPa) es 3.31 veces superior al del ladrillo macizo tipo A (σadm_flex=4 MPa); en este caso el ladrillo es el único material de mampostería que se puede comparar ya que el bloque de hormigón hueco no trabaja bajo el modo mecánico de flexión. Por otra parte luego de haber realizado la respectiva modelación de elementos finitos se puede asegurar que en los biotableros estructurales tipo sándwich no se presentaron fallas dentro o fuera del plano bajo las cargas aplicadas; la falla fuera del plano no se presentó debido a que los paneles externos de bambú le dieron la rigidez necesaria al sistema; a su vez, tampoco se presentaron fallas en el plano por corte o aplastamiento, ya que los tableros externos al ser bidireccionales disipan la fuerza de corte y el núcleo de balsa permite la trasferencia de la fuerza hacia los dos paneles sin necesidad de deformarse.
Los hallazgos de esta investigación demuestran que los prototipos de tableros estructurales compuestos tipo sándwich satisfacen plenamente requisitos de ingeniería para su uso estructural en edificaciones debido a su bajo peso, alta resistencia a esfuerzos internos y externos, gran flexibilidad y ductilidad, producción sostenible, facilidad de transporte y sobre todo bajo impacto ambiental.
Pese a que los resultados del presente estudio cumplen con el alcance de la investigación propuesta, es necesario complementarlo con pruebas de (i) amortiguamiento y vibración (ASTM E576), (ii) resistencia a la fatiga (ASTM C393, 2011) que presentan los prototipos ante cargas dinámicas, (iii) respuesta ante la acción del fuego (Normativa chilena, NCh 395), (iv) absorción de sonido (ASTM E1050, 2012), y (v) conductividad térmica (ASTM C177, 2019).
Hibsch C., Alvarado A., Yepes H., Sebrier M. & Pérez H.,(1996) "Falla Activa de Quito y Fuentes Sismogenéticas Regionales: Un estudio del Riesgo Sísmico de Quito con el Análisis de los sedimentos cuaternarios", Bulletin de l´Institut Francais d´Études Andines, ISSN: 2076-5827.
Rivadeneira F., Segovia M., Alvarado A., Egred J., Troncoso L., Vaca S. & Yepes H.,(2007)."Breves fundamentos sobre los terremotos en el Ecuador". C. E. Nacional, ISBN: 978-9978-84-460-1.
Stein S. & Wysession M.,(2009)."An introduction to seismology, earthquakes, and earth structure". ISBN: 978-0- 86542-078-6.
Secretaria de Gestion de Riesgos.(2016)."Informe de Situación. In: RIESGOS, S.D.G.D. (ed)".
Páez D.,(2016) "Influencia de muros de mampostería en el comportamiento de edificios de Manta durante el terremoto de 16 de abril del 2016, Pedernales-Ecuador", Revista Internacional de Ingeniería de Estructuras, (Volumen 3), ISSN: 1390-0315.
Ministerio del Ambiente.(2014)."Sistema de Contabilidad Ambiental Nacional Exploración Inicial". ISBN: 978-9942- 07-828-5.
Lippke B., Wilson J., Meil J. & Taylor A.,(2010) "Characterizing the importance of carbon stored in wood products", Wood and Fiber Science, (Volumen 42), ISSN: 0735-6161, 5-14 pp.
McKeever D.B.,(1997)."Engineered wood products: a response to the changing timber resource". 15.
Salazar V.H.,(2014)."Vivienda con estructura de madera en la ciudad de guayaquil. "
ASTM C364.(2016)."Standard Test Method for Edgewise Compressive Strength of Sandwich Constructions".
Ugural A.C.,(2008)."Mechanics of materials". Unitated States: New jersey Institute of Technology, ISBN: 9780471721154, 716 pp.
ASTM C297.(2004)."Standard Test Method for Flatwise Tensile Strength of Sandwich Constructions".
ASTM C273.(2000)."Standard Test Method For Shear Properties of Sandwich Core Materials".
Carrillo J.C.J. & González G.,(2007) "Modelación inelástica de pórticos de concreto con mampostería no reforzada", Dyna, (Volumen 74), ISSN: 2346-2183, 229-239 pp.
MVarela-Rivera J.L., Chan-Esquivel S., Fernández-Baqueiro L.E. & Moreno-Herrera J.A.,(2015) "Comportamiento de muros de mampostería confinada con aberturas sujetos a cargas fuera del plano", Concreto y cemento. Investigación y desarrollo, (Volumen 7), ISSN: 2007-3011, 52-65 pp.
Garbin E., Galati N., Nanni A., Modena C. & Valluzzi M.R.,(2007)."Provisional design guidelines for the strengthening of masonry structures subject to in-plane loading". 3-5 pp.
Davies J.,(1987) "Design criteria for structural sandwich panels", Structural Engineer. Part A, (Volumen 65), ISSN: 0151-9462, 435 pp.
Ross R.J.,(2010)."Wood handbook: wood as an engineering material".
Hull D. & Clyne T.W.,(1996)."An introduction to composite materials". ISBN: 0521388554.
Allen H.G.,(2013)."Analysis and design of structural sandwich panels: the commonwealth and international library: structures and solid body mechanics division". First Edition, ISBN: 978-0-08-012870-2.
Terradillos López A.,(2018)."Diseño y fabricación de una barra flexible para un dispositivo de rehabilitación de torso".
Heiko J. & Barbu M.,(2010)."Light Weight Panels: Summary of a New Development in Europe". Taipei-China.
González O.,(2016) "Influence of density distribution on the mechanical efficiency of coconut stem green tissues".
González O.,(2018)."The Ingenious Tree of Life - A biomechanical Approach to Cocowood Science". ISBN: 9786139870004.
ASTM E576.(2014)."Standard Test Method for Frost/Dew Point of Sealed Insulating Glass Units in the Vertical Position".
ASTM C393.(2011)."Standard Test Method for Core Shear Properties of Sandwich Constructions by Beam Flexure".
ASTM E1050.(2012)."Standard Test Method for Impedance and Absorption of Acoustical Materials Using a Tube, Two Microphones and a Digital Frequency Analysis System".
ASTM C177.(2019)."Standard Test Method for Steady-State Heat Flux Measurements and Thermal Transmission Properties by Means of the Guarded-Hot-Plate Apparatus".

![]()
© Universidad de las Fuerzas Armadas ESPE Sangolquí, Ecuador. CIENCIA - QUITO, Volumen 22, No. 1, Enero 2020
ISSN: 1390-1117, ISSN en línea: xxx-xxx.
Revista Trimestral- 50 ejemplares
“THIS IS AN OPEN ACCESS ARTICLE UNDER THE TERMS OF THE CREATIVE COMMONS ATTRIBUTION LICENSE, WHICH PERMITS USE, DISTRIBUTION AND REPRODUCTION IN ANY MEDIUM, PROVIDED THE ORIGINAL WORK IS PROPERLY CITED.”