On the performance improvement of the optimal-sampling-inspired self-triggered control at implementation stage
Main Article Content
Abstract
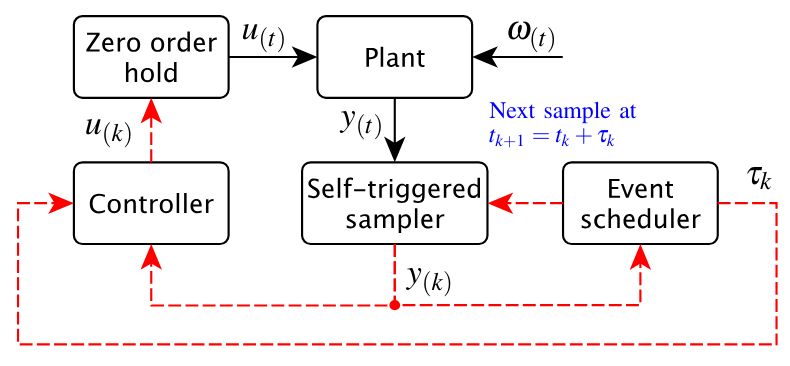
The self-triggered control includes a sampling strategy that focuses on decreasing the use of computational resources (processor and network) while preserving the same control performance as the one obtained via a controller with periodic sampling. This framework recently developed a self-triggered control technique inspired by a sampling pattern whose optimal density minimizes the control cost. This approach is called “optimal-sampling-inspired self-triggered control.” However, the strategies used to implement it on microprocessor-controlled systems working under perturbation are still unclear; this paper addresses some techniques to organize and improve the implementation on actual controllers. The proposed solution comprises the formulation of two algorithms to organize the implementation and the insertion of a closed-loop observer to deal with the perturbation that usually appears on natural plants. Regarding the former, specific computationally expensive processes involved in implementing this control technique are treated through their replacement by lightweight polynomials fitted at the design stage. Simulations and practical experiments confirm the solution is effective, and there could be an open research topic concerning observation in optimal-sampling self-triggered control strategies.
Downloads
Article Details

This work is licensed under a Creative Commons Attribution 4.0 International License.
Authors who publish in this journal agree to the following terms: Authors retain the copyright and guarantee the journal the right to be the first publication of the work, as well as, licensed under a Creative Commons Attribution License that allows others share the work with an acknowledgment of the authorship of the work and the initial publication in this journal. Authors may separately establish additional agreements for the non-exclusive distribution of the version of the work published in the journal (for example, placing it in an institutional repository or publishing it in a book), with acknowledgment of its initial publication in this journal. Authors are allowed and encouraged to disseminate their work electronically (for example, in institutional repositories or on their own website) before and during the submission process, as it may lead to productive exchanges as well as further citation earliest and oldest of published works.
How to Cite
References
[2] A. Anta and P. Tabuada, “To Sample or Not to Sample: Self-Triggered Control for Nonlinear Systems,” IEEE Trans. Autom. Control, vol. 55, no. 9, pp. 2030-2042, Sept. 2010.
[3] M. Mazo Jr., A. Anta and P. Tabuada, “An ISS Self-Triggered Implementation of Linear Controllers,” in Automatica, vol. 46, no. 8, pp. 1310-1314, Aug. 2010.
[4] J. Almeida, C. Silvestre and A.M. Pascoal, “Self-Triggered Output Feedback Control of Linear Plants,” in Proc. ACC, San Francisco, CA, USA, June-July, 2011, pp. 2831-2836.
[5] A. Molin and S. Hirche, ”On the Optimality of Certainty Equivalence for Event-Triggered Control Systems”, in IEEE Trans. Autom. Control, vol. 58, no. 2, pp. 470-474, Feb. 2013.
[6] E. Bini and G.M. Buttazzo, “The Optimal Sampling Pattern For Linear Control Systems,” in IEEE Trans. Autom. Control, vol. 59, no. 1, pp. 78-90, Jan. 2014.
[7] M. Velasco, P. Mart´ı and E. Bini, “Optimal-Sampling-inspired Self-Triggered Control,” in Int. Conf. EBCCSP, Krakow, Poland, June, 2015, pp. 1-8.
[8] K.J. A° stro¨m and B. Wittenmark, Computer-Controlled Systems: Theory and Design, 3rd ed., Upper Saddle River, NJ, USA: Prentice Hall, 1997.
[9] T. Gommans, D. Antunes, T. Donkers, P. Tabuada, and M. Heemels, ”Self-Triggered Linear Quadratic Control”, in Automatica, vol. 50, no. 4, pp. 1279-1287, Apr. 2014.
[10] C. Rosero, C. Vaca, L. Tobar and F. Rosero, “Performance of Self-Triggered Control Approaches,” in Enfoque UTE, vol. 8, no. 2, pp. 107-120, Mar. 2017.
[11] J. Almeida, C. Silvestre and A.M. Pascoal, “Observer Based Self-Triggered Control of Linear Plants with Unknown Disturbances,” in Proc. ACC, Montreal, Canada, June, 2012, pp. 5688-5693.
[12] X. Wang and M.D. Lemmon, “Self-Triggering Under State-Independent Disturbances,” in IEEE Trans. Autom. Control, vol. 55, no. 6, pp. 1494-1500, June 2010.
[13] W.F. Arnold and A.J. Laub, “Generalized Eigenproblem Algorithms and Software for Algebraic Riccati Equations,” in Proc. IEEE, vol. 72, no. 12, pp. 1746-1754, Dec. 1984.
[14] D. Luenberger, “An Introduction to Observers,” in IEEE Trans. Autom. Control, vol. 16, no. 6, pp. 596-602, Dec. 1971.
[15] J. Ackermann, “On the Synthesis of Linear Control Systems with Specified Characteristics,” in Automatica, vol. 13, no. 1, pp. 89-94, Jan. 1977.
[16] F. Paez, R. Cayssials, J. Urriza, E. Ferro and J. Orozco, “Frequency Domain Analysis of a RTOS in Control Applications,” in Cong. CASE, Buenos Aires, Argentina, Aug., 2016, pp. 21-26.
[17] S.A. Dyer and X. He, “Least-squares fitting of data by polynomials,” in IEEE Instrum. Meas. Mag., vol. 4, no. 4, pp. 46-51, Dec. 2001.
[18] C. Lozoya, P. Mart´ı, M. Velasco, J. Fuertes and E. Martin, “Resource and Performance Trade-offs in Real-Time Embedded Control Systems,” in J. Real-Time Systems, vol. 49, no. 3, pp. 267-307, May 2013.