Control QFT en tiempo real para la temperatura en invernaderos
Barra lateral del artículo
Publicado:
May 24, 2019
Palabras clave:
Controlador QFT, control robusto, control de temperatura, predictor Smith
Contenido principal del artículo
Resumen
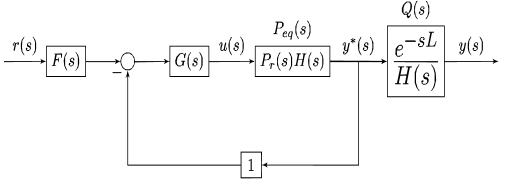
Los cambios repentinos en el ambiente del invernadero tienen un impacto negativo en el desarrollo y la producción de cultivos, especialmente en invernaderos con ventilación natural cuando las temperaturas son bajas en la noche y cambian rápidamente debido a los vientos húmedos. Para mitigar estas variaciones, se propone el diseño de un controlador robusto basado en la Teoría de Realimentación Cuantitativa, (por su sigla en inglés QFT), a partir de una estructura tipo predictor de Smith para sistemas con tiempo muerto. Este esquema ofrece una alta estabilidad basada en el margen de ganancia, el margen de fase y el rechazo de las perturbaciones en la salida del sistema. El diseño se contrastó con un controlador PID basado en índices de desempeño, de acuerdo con la respuesta transitoria y el error ante la presencia de cambios en el punto de operación y las perturbaciones de carga. Los resultados finales mostraron que la respuesta dinámica del controlador QFT mejoró en comparación con los resultados del controlador PID.
Detalles del artículo
Cómo citar
Control QFT en tiempo real para la temperatura en invernaderos. (2019). MASKAY, 9(2), 58-62. https://doi.org/10.24133/maskay.v9i2.1162
Número
Sección
ARTÍCULOS TÉCNICOS
Esta obra está bajo una licencia internacional Creative Commons Atribución 4.0.
Los autores que publican en esta revista están de acuerdo con los siguientes términos: Los autores conservan los derechos de autor y garantizan a la revista el derecho de ser la primera publicación del trabajo al igual que licenciado bajo una Creative Commons Attribution License que permite a otros compartir el trabajo con un reconocimiento de la autoría del trabajo y la publicación inicial en esta revista. Los autores pueden establecer por separado acuerdos adicionales para la distribución no exclusiva de la versión de la obra publicada en la revista (por ejemplo, situarlo en un repositorio institucional o publicarlo en un libro), con un reconocimiento de su publicación inicial en esta revista. Se permite y se anima a los autores a difundir sus trabajos electrónicamente (por ejemplo, en repositorios institucionales o en su propio sitio web) antes y durante el proceso de envío, ya que puede dar lugar a intercambios productivos, así como a una citación más temprana y mayor de los trabajos publicados.Cómo citar
Control QFT en tiempo real para la temperatura en invernaderos. (2019). MASKAY, 9(2), 58-62. https://doi.org/10.24133/maskay.v9i2.1162
Referencias
[1] K. Yingchun and S. Yue, “A Greenhouse Temperature and Humidity Controller Based on MIMO Fuzzy System,” in 2010 International Conference on Intelligent System Design and Engineering Application, 2010, vol. 1, pp. 35–39.
[2] A. Visioli and Q. Zhong, Control of Integral Processes with Dead Time. London: Springer-Verlag, 2011.
[3] Z. D. Tian, “Algorithm and Implementation of Smith Predictive Control,” Appl. Mech. Mater., vol. 687–691, pp. 60–63, Nov. 2014.
[4] E. H. Gurban and G.-D. Andreescu, “Comparison of modified Smith predictor and PID controller tuned by genetic algorithms for greenhouse climate control,” 2014, pp. 79–83.
[5] S. A. C. Giraldo, R. C. C. Flesch, and J. E. Normey-Rico, “Multivariable Greenhouse Control Using the Filtered Smith Predictor,” J. Control Autom. Electr. Syst., vol. 27, no. 4, pp. 349–358, Aug. 2016.
[6] C. Esparza, R. Núñez, and F. González, “Model Reference Adaptive Position Controller with Smith Predictor for a Shaking-Table in Two Axes,” in Advances in Computational Intelligence, 2012, pp. 271–282.
[7] J. M. B. García, A. A. García, and E. F. Amorós, Electrónica de potencia: teoría y aplicaciones. Universidad Politécnica de Valencia. Servicio de Publicaciones, 1999.
[8] M. Garcia-Sanz and C. H. Houpis, Wind Energy Systems: Control Engineering Design. CRC Press, 2012.
[9] A. H. Ahmadi and S. K. Y. Nikravesh, “Robust Smith Predictor (RSP),” in 2016 24th Iranian Conference on Electrical Engineering (ICEE), 2016, pp. 1510–1515.
[10] V. M. Alfaro and R. Vilanova, Model-Reference Robust Tuning of PID Controllers. Cham: Springer International Publishing, 2016.
[11] F. N. Deniz and N. Tan, “A Model Identification Method for Tuning of PID Controller in a Smith Predictor Structure,” IFAC-Pap., vol. 49, no. 10, pp. 13–18, Jan. 2016.
[12] F. S. S. de Oliveira, F. O. Souza, and R. M. Palhares, “PID Tuning for Time-Varying Delay Systems Based on Modified Smith Predictor 11This work has been supported by the Brazilian agencies CAPES, CNPq, and FAPEMIG.,” IFAC-Pap., vol. 50, no. 1, pp. 1269–1274, Jul. 2017.
[13] M. Garcia-Sanz and J. G. Guillen, “Smith predictor for uncertain systems in the QFT framework,” in Progress in system and robot analysis and control design, Springer, London, 1999, pp. 239–250.
[14] M. Garcia-Sanz, Robust Control Engineering: Practical QFT Solutions. CRC Press, 2017.
[15] M. G. Martínez, “Síntesis de controladores robustos mediante el análisis de la compatibilidad de especificaciones e incertidumbre,” http://purl.org/dc/dcmitype/Text, Universidad Pública de Navarra, 2001.
[16] C. H. Houpis, S. N. Sheldon, and J. J. D’Azzo, Linear Control System Analysis and Design: Fifth Edition, Revised and Expanded. CRC Press, 2003.
[17] N. Cohen, Y. Chait, O. Yaniv, and C. Borghesani, “Stability analysis using Nichols charts,” Int. J. Robust Nonlinear Control, vol. 4, no. 1, pp. 3–20, 1994.
[18] J. Elso, M. Gil-Martinez, and M. Garcia-Sanz, “Quantitative feedback control for multivariable model matching and disturbance rejection,” Int. J. Robust Nonlinear Control, vol. 27, no. 1, pp. 121–134, Jan. 2017.
[19] M. Gil-Martínez and M. García-Sanz, “Simultaneous meeting of robust control specifications in QFT,” Int. J. Robust Nonlinear Control, vol. 13, no. 7, pp. 643–656, 2003.
[20] Y. Chait and O. Yaniv, “Multi-input/single-output computer-aided control design using the quantitative feedback theory,” Int. J. Robust Nonlinear Control, vol. 3, no. 1, pp. 47–54, Jan. 1993.
[21] A. Visioli, Practical PID Control. London: Springer-Verlag, 2006.
[2] A. Visioli and Q. Zhong, Control of Integral Processes with Dead Time. London: Springer-Verlag, 2011.
[3] Z. D. Tian, “Algorithm and Implementation of Smith Predictive Control,” Appl. Mech. Mater., vol. 687–691, pp. 60–63, Nov. 2014.
[4] E. H. Gurban and G.-D. Andreescu, “Comparison of modified Smith predictor and PID controller tuned by genetic algorithms for greenhouse climate control,” 2014, pp. 79–83.
[5] S. A. C. Giraldo, R. C. C. Flesch, and J. E. Normey-Rico, “Multivariable Greenhouse Control Using the Filtered Smith Predictor,” J. Control Autom. Electr. Syst., vol. 27, no. 4, pp. 349–358, Aug. 2016.
[6] C. Esparza, R. Núñez, and F. González, “Model Reference Adaptive Position Controller with Smith Predictor for a Shaking-Table in Two Axes,” in Advances in Computational Intelligence, 2012, pp. 271–282.
[7] J. M. B. García, A. A. García, and E. F. Amorós, Electrónica de potencia: teoría y aplicaciones. Universidad Politécnica de Valencia. Servicio de Publicaciones, 1999.
[8] M. Garcia-Sanz and C. H. Houpis, Wind Energy Systems: Control Engineering Design. CRC Press, 2012.
[9] A. H. Ahmadi and S. K. Y. Nikravesh, “Robust Smith Predictor (RSP),” in 2016 24th Iranian Conference on Electrical Engineering (ICEE), 2016, pp. 1510–1515.
[10] V. M. Alfaro and R. Vilanova, Model-Reference Robust Tuning of PID Controllers. Cham: Springer International Publishing, 2016.
[11] F. N. Deniz and N. Tan, “A Model Identification Method for Tuning of PID Controller in a Smith Predictor Structure,” IFAC-Pap., vol. 49, no. 10, pp. 13–18, Jan. 2016.
[12] F. S. S. de Oliveira, F. O. Souza, and R. M. Palhares, “PID Tuning for Time-Varying Delay Systems Based on Modified Smith Predictor 11This work has been supported by the Brazilian agencies CAPES, CNPq, and FAPEMIG.,” IFAC-Pap., vol. 50, no. 1, pp. 1269–1274, Jul. 2017.
[13] M. Garcia-Sanz and J. G. Guillen, “Smith predictor for uncertain systems in the QFT framework,” in Progress in system and robot analysis and control design, Springer, London, 1999, pp. 239–250.
[14] M. Garcia-Sanz, Robust Control Engineering: Practical QFT Solutions. CRC Press, 2017.
[15] M. G. Martínez, “Síntesis de controladores robustos mediante el análisis de la compatibilidad de especificaciones e incertidumbre,” http://purl.org/dc/dcmitype/Text, Universidad Pública de Navarra, 2001.
[16] C. H. Houpis, S. N. Sheldon, and J. J. D’Azzo, Linear Control System Analysis and Design: Fifth Edition, Revised and Expanded. CRC Press, 2003.
[17] N. Cohen, Y. Chait, O. Yaniv, and C. Borghesani, “Stability analysis using Nichols charts,” Int. J. Robust Nonlinear Control, vol. 4, no. 1, pp. 3–20, 1994.
[18] J. Elso, M. Gil-Martinez, and M. Garcia-Sanz, “Quantitative feedback control for multivariable model matching and disturbance rejection,” Int. J. Robust Nonlinear Control, vol. 27, no. 1, pp. 121–134, Jan. 2017.
[19] M. Gil-Martínez and M. García-Sanz, “Simultaneous meeting of robust control specifications in QFT,” Int. J. Robust Nonlinear Control, vol. 13, no. 7, pp. 643–656, 2003.
[20] Y. Chait and O. Yaniv, “Multi-input/single-output computer-aided control design using the quantitative feedback theory,” Int. J. Robust Nonlinear Control, vol. 3, no. 1, pp. 47–54, Jan. 1993.
[21] A. Visioli, Practical PID Control. London: Springer-Verlag, 2006.